队列:先入先出的数据结构
设计循环队列
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
- MyCircularQueue(k): 构造器,设置队列长度为 k 。
- Front: 从队首获取元素。如果队列为空,返回 -1 。
- Rear: 获取队尾元素。如果队列为空,返回 -1 。
- enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
- deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
- isEmpty(): 检查循环队列是否为空。
- isFull(): 检查循环队列是否已满。
题解:
class MyCircularQueue {
private int[] data;
private int front, tail;
public MyCircularQueue(int k) {
data = new int[k + 1];
front = 0;
tail = 0;
}
public boolean enQueue(int value) {
if (isFull()) {
return false;
} else {
data[tail] = value;
tail = (tail + 1) % data.length;
return true;
}
}
public boolean deQueue() {
if (isEmpty()) {
return false;
} else {
front = (front + 1) % data.length;
return true;
}
}
public int Front() {
if (isEmpty()) {
return -1;
}
return data[front];
}
public int Rear() {
if (isEmpty()) {
return -1;
}
return data[(tail - 1 + data.length) % data.length];
}
public boolean isEmpty() {
return front == tail;
}
public boolean isFull() {
return (tail + 1) % data.length == front;
}
}队列与广度优先搜索
岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3题解1:(DFS)
class Solution {
public int numIslands(char[][] grid) {
if(grid.length==0||grid==null) {
return 0;
}
int count = 0;
for(int i=0;i<grid.length;i++) {
for(int j=0;j<grid[0].length;j++) {
if(grid[i][j]=='1') {
count++;
dfs(grid, i, j);
}
}
}
return count;
}
public void dfs(char[][] grid, int i, int j) {
if(i<0||j<0||i>=grid.length||j>=grid[0].length) {
return ;
}
if(grid[i][j]=='1') {
grid[i][j] = '0';
dfs(grid, i-1, j);
dfs(grid, i+1, j);
dfs(grid, i, j-1);
dfs(grid, i, j+1);
}else{
return ;
}
}
}题解2:(BFS)
class Solution {
public int numIslands(char[][] grid) {
if(grid.length==0||grid==null) {
return 0;
}
int count = 0;
for(int i=0;i<grid.length;i++) {
for(int j=0;j<grid[0].length;j++) {
if(grid[i][j]=='1') {
count++;
grid[i][j] = 0;
bfs(grid, i, j);
}
}
}
return count;
}
public void bfs(char[][] grid, int x, int y) {
int rowLen = grid.length;
int colLen = grid[0].length;
Queue <Integer> queue = new LinkedList<>();
int code = x*colLen+y;
queue.add(code);
while(!queue.isEmpty()) {
code = queue.poll();
int i = code/colLen;
int j = code%colLen;
if(i>0&&grid[i-1][j]=='1') {
grid[i-1][j] = 0;
queue.add((i-1)*colLen+j);
}
if(i<rowLen-1&&grid[i+1][j]=='1') {
grid[i+1][j] = 0;
queue.add((i+1)*colLen+j);
}
if(j>0&&grid[i][j-1]=='1') {
grid[i][j-1] = 0;
queue.add(i*colLen+j-1);
}
if(j<colLen-1&&grid[i][j+1]=='1') {
grid[i][j+1] = 0;
queue.add(i*colLen+j+1);
}
}
}
}打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:把最后一位反向旋转一次即可 "0000" -> "0009"。示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:无法旋转到目标数字且不被锁定。提示:
1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target 不在 deadends 之中
target 和 deadends[i] 仅由若干位数字组成
题解:(BFS)
class Solution {
public int openLock(String[] deadends, String target) {
Set<String> set = new HashSet<>(Arrays.asList(deadends));
//开始遍历的字符串是"0000",相当于根节点
String startStr = "0000";
if (set.contains(startStr))
return -1;
//创建队列
Queue<String> queue = new LinkedList<>();
//记录访问过的节点
Set<String> visited = new HashSet<>();
queue.offer(startStr);
visited.add(startStr);
//树的层数
int level = 0;
while (!queue.isEmpty()) {
//每层的子节点个数
int size = queue.size();
while (size-- > 0) {
//每个节点的值
String str = queue.poll();
//对于每个节点中的4个数字分别进行加1和减1,相当于创建8个子节点,这八个子节点
//可以类比二叉树的左右子节点
for (int i = 0; i < 4; i++) {
char ch = str.charAt(i);
//strAdd表示加1的结果,strSub表示减1的结果
String strAdd = str.substring(0, i) + (ch == '9' ? 0 : ch - '0' + 1) + str.substring(i + 1);
String strSub = str.substring(0, i) + (ch == '0' ? 9 : ch - '0' - 1) + str.substring(i + 1);
//如果找到直接返回
if (str.equals(target))
return level;
//不能包含死亡数字也不能包含访问过的字符串
if (!visited.contains(strAdd) && !set.contains(strAdd)) {
queue.offer(strAdd);
visited.add(strAdd);
}
if (!visited.contains(strSub) && !set.contains(strSub)) {
queue.offer(strSub);
visited.add(strSub);
}
}
}
//当前层访问完了,到下一层,层数要加1
level++;
}
return -1;
}
}完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9题解:
class Solution {
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
queue.offer(0);
visited.add(0);
int level = 0;
while(!queue.isEmpty()) {
int size = queue.size();
level++;
for(int i=0;i<size;i++) {
int node = queue.poll();
for(int j=1;j<=n;j++) {
int sum = node + j*j;
if(sum==n) {
return level;
}
if(sum>n) {
break;
}
if(!visited.contains(sum)) {
queue.offer(sum);
visited.add(sum);
}
}
}
}
return level;
}
}栈:后入先出的数据结构
模板:
// "static void main" must be defined in a public class.
public class Main {
public static void main(String[] args) {
// 1. Initialize a stack.
Stack<Integer> s = new Stack<>();
// 2. Push new element.
s.push(5);
s.push(13);
s.push(8);
s.push(6);
// 3. Check if stack is empty.
if (s.empty() == true) {
System.out.println("Stack is empty!");
return;
}
// 4. Pop an element.
s.pop();
// 5. Get the top element.
System.out.println("The top element is: " + s.peek());
// 6. Get the size of the stack.
System.out.println("The size is: " + s.size());
}
}最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
示例 1:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.提示:
-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 104 次
题解1:(辅助类)
class MinStack {
private ListNode head;
public MinStack() {}
public void push(int val) {
if(empty()) {
head = new ListNode(val, val, null);
} else {
head = new ListNode(val, Math.min(val, head.min), head);
}
}
public void pop() {
if(!empty()) {
head = head.next;
}
}
public int top() {
if(!empty()) {
return head.val;
} else {
throw new IllegalStateException();
}
}
public int getMin() {
if(!empty()) {
return head.min;
} else {
throw new IllegalStateException();
}
}
public boolean empty() {
return head == null;
}
}
class ListNode {
public int val;
public int min;
public ListNode next;
public ListNode(int val, int min, ListNode next) {
this.val = val;
this.min = min;
this.next = next;
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/题解2:(单栈)
public class MinStack {
long min;
Stack<Long> stack = new Stack<>();
public void push(int x) {
if (stack.isEmpty()) {
stack.push(0L);
min = x;
} else {
//这里入栈的是入栈的值和最小值的差值,有可能为负,也有可能为正。
stack.push(x - min);
if (x < min)
min = x;
}
}
public void pop() {
if (stack.isEmpty())
return;
long pop = stack.pop();
//因为入栈的是差值,当出栈的为负数的时候,说明栈中最小值已经出栈了,
//这里要重新更新最小值
if (pop < 0)
min -= pop;
}
public int top() {
long top = stack.peek();
if (top > 0) {
//栈顶元素如果是正的,说明栈顶元素压栈的时候是比栈中最小值大的,根据
//top=x - min,可以计算x=top+min
return (int) (top + min);
} else {
//当栈顶元素是负数的时候,说明栈顶元素压栈的时候是比栈中最小值小的,
//而压栈完之后他会更新最小值min,所以如果在使用上面公式肯定是不行
//的。如果栈顶元素压栈的时候比最小值小,他会更新最小值,这个最小值
//就是我们要压栈的值,所以这里直接返回min就行了。
return (int) (min);
}
}
public int getMin() {
return (int) min;
}
}题解3:(双栈)
class MinStack {
//栈1存放的是需要压栈的值
Stack<Integer> stack1 = new Stack<>();
//栈2存放的是最小值
Stack<Integer> stack2 = new Stack<>();
public void push(int x) {
stack1.push(x);
if (stack2.empty() || x <= getMin())
stack2.push(x);
}
public void pop() {
//如果出栈的值等于最小值,说明栈中的最小值
//已经出栈了,因为stack2中的栈顶元素存放的
//就是最小值,所以stack2栈顶元素也要出栈
if (stack1.pop() == getMin())
stack2.pop();
}
public int top() {
return stack1.peek();
}
public int getMin() {
return stack2.peek();
}
}有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()"
输出:true示例 2:
输入:s = "()[]{}"
输出:true示例 3:
输入:s = "(]"
输出:false提示:
1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成
题解:
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
char[] chars = s.toCharArray();
for (char c : chars) {
if (c == '(') {
stack.push(')');
} else if (c == '{') {
stack.push('}');
} else if (c == '[') {
stack.push(']');
} else if (stack.isEmpty() || stack.pop() != c) {
return false;
}
}
return stack.isEmpty();
}
}每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]提示:
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100
解法1:(倒序遍历)
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int len = temperatures.length - 1;
int[] res = new int[len+1];
for(int i=len;i>=0;i--) {
int j=i+1;
while(j<len+1) {
if(temperatures[i] < temperatures[j]) {
res[i] = j-i;
break;
} else if(res[j]==0) {
break;
} else {
j += res[j];
}
}
}
return res;
}
}解法2:(栈)
class Solution {
public int[] dailyTemperatures(int[] T) {
Stack<Integer> stack = new Stack<>();
int[] nums = new int[T.length];
for(int i=0;i<T.length;i++) {
while(!stack.isEmpty() && T[i]>T[stack.peek()]) {
int index = stack.pop();
nums[index] = i-index;
}
stack.push(i);
}
return nums;
}
}逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22提示:
1 <= tokens.length <= 104
tokens[i] 是一个算符("+"、"-"、"*" 或 "/"),或是在范围 [-200, 200] 内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
题解:
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for(String token:tokens) {
int a,b;
if(token.equals("+")) {
a=stack.pop();
b=stack.pop();
stack.push(a + b);
} else if(token.equals("-")) {
a=stack.pop();
b=stack.pop();
stack.push(b - a);
} else if(token.equals("*")) {
a=stack.pop();
b=stack.pop();
stack.push(b * a);
} else if(token.equals("/")) {
a=stack.pop();
b=stack.pop();
stack.push(b / a);
} else {
stack.push(Integer.parseInt(token));
}
}
return stack.pop();
}
}栈和深度优先搜索
BFS模板:
/*
* Return true if there is a path from cur to target.
*/
boolean DFS(Node cur, Node target, Set<Node> visited) {
return true if cur is target;
for (next : each neighbor of cur) {
if (next is not in visited) {
add next to visted;
return true if DFS(next, target, visited) == true;
}
}
return false;
}克隆图
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
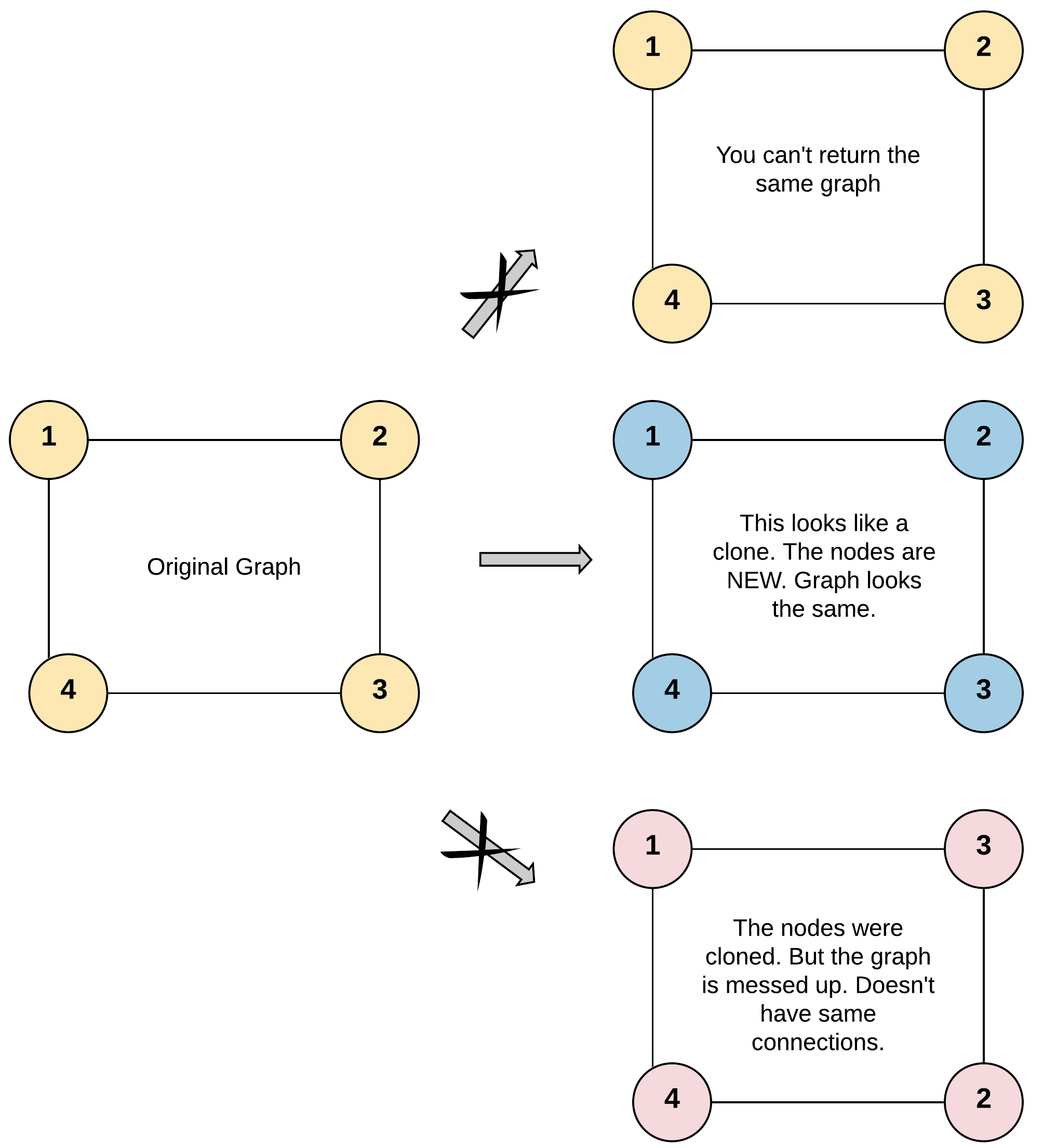
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。示例 2:
输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。示例 4:
输入:adjList = [[2],[1]]
输出:[[2],[1]]提示:
节点数不超过 100 。
每个节点值 Node.val 都是唯一的,1 <= Node.val <= 100。
无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
图是连通图,你可以从给定节点访问到所有节点。
题解:
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
class Solution {
public Node cloneGraph(Node node) {
return clone(node, new HashMap<>());
}
public Node clone(Node node, HashMap<Integer, Node> visited) {
//边界条件判断
if (node == null)
return null;
//如果当前节点已经创建了,直接返回
if (visited.containsKey(node.val))
return visited.get(node.val);
//否则创建当前节点
Node newNode = new Node(node.val, new ArrayList<>());
//把创建的节点存放到map中
visited.put(newNode.val, newNode);
//创建当前节点的邻居节点
for (Node neighbor : node.neighbors)
newNode.neighbors.add(clone(neighbor, visited));
return newNode;
}
}目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3示例 2:
输入:nums = [1], target = 1
输出:1提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
题解:(二叉树)
class Solution {
int count = 0;
public int findTargetSumWays(int[] nums, int target) {
dfs(nums, target, -1, 0);
return count;
}
public void dfs(int[] nums, int target, int i, int sum) {
if(i < nums.length-1) {
dfs(nums, target, i+1, sum-nums[i+1]);
dfs(nums, target, i+1, sum+nums[i+1]);
} else {
if (target == sum) {
count++;
}
return ;
}
}
}二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:

输入:root = [1,null,2,3]
输出:[1,3,2]示例 2:
输入:root = []
输出:[]示例 3:
输入:root = [1]
输出:[1]代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
List<Integer> res = new ArrayList<Integer>();
while(root != null || !stack.isEmpty()){
while(root!=null){ // 不断地向左结点深入,直至叶子结点
stack.push(root);
root = root.left;
}
TreeNode top = stack.pop();
res.add(top.val);
root = top.right;
}
return res;
}
}小结
用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
- void push(int x) 将元素 x 推到队列的末尾
- int pop() 从队列的开头移除并返回元素
- int peek() 返回队列开头的元素
- boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例1:
输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]
解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false提示:
- 1 <= x <= 9
- 最多调用 100 次 push、pop、peek 和 empty
- 假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)
进阶:
你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。
class MyQueue {
private Deque<Integer> stack1;
private Deque<Integer> stack2;
public MyQueue() {
stack1 = new ArrayDeque<>();
stack2 = new ArrayDeque<>();
}
public void push(int x) {
stack1.push(x);
}
public int pop() {
fillStack();
return stack2.pop();
}
public int peek() {
fillStack();
return stack2.peek();
}
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
}
public void fillStack() {
if(stack2.isEmpty()) {
while(!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
- 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
- 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入:
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]
解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False提示:
- 1 <= x <= 9
- 最多调用100 次 push、pop、top 和 empty
- 每次调用 pop 和 top 都保证栈不为空
进阶:你能否仅用一个队列来实现栈。
题解1:(双队列)
class MyQueue {
private Deque<Integer> stack1;
private Deque<Integer> stack2;
public MyQueue() {
stack1 = new ArrayDeque<>();
stack2 = new ArrayDeque<>();
}
public void push(int x) {
stack1.push(x);
}
public int pop() {
fillStack();
return stack2.pop();
}
public int peek() {
fillStack();
return stack2.peek();
}
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
}
public void fillStack() {
if(stack2.isEmpty()) {
while(!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/题解2:(单队列)
public class MyStack {
//简单单队列实现栈
Queue<Integer> one;
public MyStack() {
one=new LinkedList<>();
}
/**在添加元素之前得到原本队列的大小;
* 再添加新元素,然后把开头的元素调到最后,实现新元素在前,
* 也就是先进后出*/
public void push(int x) {
int a=one.size();
one.offer(x);
for (int i=0;i<a;i++){
one.offer(one.poll());
}
}
/**直接调用队列中删除队列中第一个元素并返回其值的方法*/
public int pop() {
return one.poll();
}
/**直接调用队列中得到第一个元素值的方法*/
public int top() {
return one.peek();
}
/**检测队列是否为空,为空则栈也为空(有不足的地方,请大家一定要指正)*/
public boolean empty() {
return one.isEmpty();
}
}字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = "3[a]2[bc]"
输出:"aaabcbc"示例 2:
输入:s = "3[a2[c]]"
输出:"accaccacc"示例 3:
输入:s = "2[abc]3[cd]ef"
输出:"abcabccdcdcdef"示例 4:
输入:s = "abc3[cd]xyz"
输出:"abccdcdcdxyz"提示:
- 1 <= s.length <= 30
- s 由小写英文字母、数字和方括号 '[]' 组成
- s 保证是一个 有效 的输入。
- s 中所有整数的取值范围为 [1, 300]
题解:
class Solution {
public String decodeString(String s) {
Deque<Integer> numStack = new ArrayDeque<>();
Deque<StringBuilder> resStack = new ArrayDeque<>();
StringBuilder res = new StringBuilder();
int num = 0;
for(char c:s.toCharArray()) {
if(Character.isDigit(c)) {
num = num*10 + c -'0';
} else if(c=='[') {
resStack.push(res);
numStack.push(num);
res = new StringBuilder();
num = 0;
} else if(c==']') {
StringBuilder str = resStack.pop();
int n = numStack.pop();
for(int i=0;i<n;i++) {
str.append(res);
}
res = str;
} else {
res.append(c);
}
}
return res.toString();
}
}01 矩阵
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
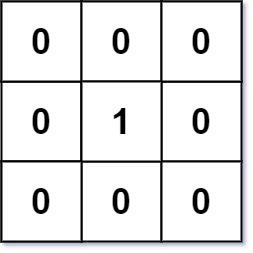
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]示例 2:
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]提示:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 104
- 1 <= m * n <= 104
- mati is either 0 or 1.
- mat 中至少有一个 0
题解:
class Solution {
public int[][] updateMatrix(int[][] mat) {
int rows = mat.length;
int cols = mat[0].length;
int[][] ans = new int[rows][cols];
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
for(int i = 0; i<rows; i++){
for(int j=0; j<cols; j++){
if(mat[i][j]==0){
queue.offer(i*cols + j);
visited.add(i*cols + j);
}
}
}
while(!queue.isEmpty()){
int size = queue.size();
for(int k = 0; k<size; k++){
int id = queue.poll();
int r = id/cols;
int c = id%cols;
if(r>0 && mat[r-1][c]==1 && !visited.contains((r-1)*cols+c)){
ans[r-1][c] = ans[r][c] + 1; // plus 1 at original location
queue.offer((r-1)*cols+c);
visited.add((r-1)*cols+c);
}if(c>0 && mat[r][c-1]==1 && !visited.contains((r)*cols+c-1)){
ans[r][c-1] = ans[r][c] + 1; // plus 1 at original location
queue.offer((r)*cols+c-1);
visited.add((r)*cols+c-1);
}if(r+1<rows && mat[r+1][c]==1 && !visited.contains((r+1)*cols+c)){
ans[r+1][c]= ans[r][c] + 1;
queue.offer((r+1)*cols+c);
visited.add((r+1)*cols+c);
}if(c+1<cols && mat[r][c+1]==1 && !visited.contains((r)*cols+c+1)){
ans[r][c+1] = ans[r][c] + 1;
queue.offer((r)*cols+c+1);
visited.add((r)*cols+c+1);
}
}
}
return ans;
}
}钥匙和房间
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
示例 1:
输入:rooms = [[1],[2],[3],[]]
输出:true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。示例 2:
输入:rooms = [[1,3],[3,0,1],[2],[0]]
输出:false
解释:我们不能进入 2 号房间。提示:
- n == rooms.length
- 2 <= n <= 1000
- 0 <= rooms[i].length <= 1000
- 1 <= sum(rooms[i].length) <= 3000
- 0 <= roomsi < n
- 所有 rooms[i] 的值 互不相同
题解:
class Solution {
private int cnt = 0;
private boolean[] visited;
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
int n = rooms.size();
visited = new boolean[n];
dfs(rooms, 0);
return cnt == n;
}
private void dfs(List<List<Integer>> rooms, int i) {
visited[i] = true;
cnt++;
for (int j : rooms.get(i)) {
if (!visited[j]) {
dfs(rooms, j);
}
}
}
}